practica 1
Författare:
MSc. Fausto M. Lagos S.
Last Updated:
för 7 år sedan
Licens:
Creative Commons CC BY 4.0
Sammanfattning:
Template for the class practice 1.

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
Template for the class practice 1.

\begin
Discover why over 25 million people worldwide trust Overleaf with their work.
%-----------------------Homework------------------------------------
%-------------------Arman Shokrollahi---------------------------------
%---------------------Coding Theory-------------------------------
\documentclass[a4 paper]{article}
% Set target color model to RGB
\input{preamble.tex}
\begin{document}
\homework{Práctia \#1}{Feb. 04 al 05 de 2019}{MSc. Fausto M. Lagos S.}{}{Aquí va su nombre}{}
En esta práctica se desarrollarán seis planteamientos cada uno con una valoración de un punto. El primero de los enunciados que encuentra resuelto es un ejemplo de cómo debe presentar la solución de los restantes enunciados planteados. El objetivo de estas práctica es afianzar sus conocimientos antes de la Prueba de Evaluación Continua correspondiente, puede utilizar todo el material bibliográfica a su disposición y también preguntar todo lo que considere necesario. Preste atención al margen derecho donde encontrará premios y bonificaciones adicionales.
\vspace{5mm}
\problem{0} \todo[color = green!50]{Esto es un ejemplo} Resuelva y represente la solución en intervalo, conjunto y sobre la recta real para la inecuación polinómica
\[
-4x^3 + 14x^2 - 4x - 6 \leq 0
\]
\solution{}
Si bien podría multiplicarse por $-1$ la incecuación planteada, el polinomio es factorizable en su versión original, habrá que tener cuidado con la inversión de la relación de orden.
\begin{paracol}{2}
La factorización del polinómio mediante la regla de Ruffini
\begin{table}[ht]
\centering
\begin{tabular}{c|cccc}
& -4 & 14 & -4 & -6 \\
\hline
3 & & -12 & 6 & 6 \\
& -4 & 2 & 2 & 0 \\
\hline
1 & & -4 & -2 & \\
& -4 & -2 & 0 &
\end{tabular}
\end{table}
\begin{gather*}
-2(x - 3)(x - 1)(2x + 1) \leq 0 \\
x \geq 3 \text{ y } x \geq 1 \text{ y } x \geq -\tfrac{1}{2}
\end{gather*}
\switchcolumn
El análisis de los signos
\begin{figure}[ht]
\centering
\begin{tikzpicture}
\reaLine{-.5}{3}
\interval{-.5}{3}{.3}{<-}{fill = none}{inf}{negative}
\interval{3}{3}{.3}{->}{fill}{inf}{positive}
\interval{-.5}{1}{.5}{<-}{fill = none}{inf}{negative}
\interval{1}{3}{.5}{->}{fill}{inf}{positive}
\interval{-0.5}{-0.5}{.7}{<-}{fill = none}{inf}{negative}
\interval{-0.5}{3}{.7}{->}{fill}{inf}{positive}
\end{tikzpicture}
\end{figure}
Tomando en cuenta el factor $-2$, el intervalo solución es:
\[
\left[-\frac{1}{2}, 1\right] \cup [3, \infty) \equiv \left\{x \in \mathbb{R} | -\frac{1}{2} \leq x \leq 1 \text{ ó } 3 \leq x\right\}
\]
\end{paracol}
\begin{paracol}{2}
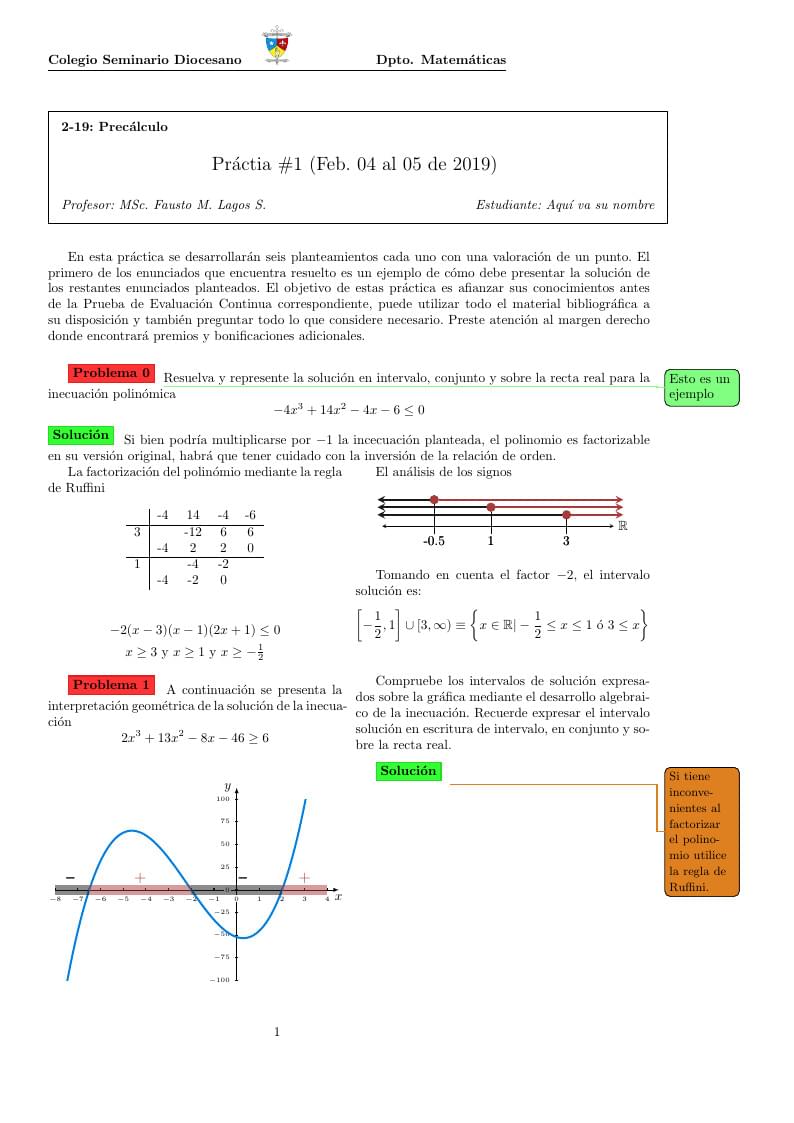
\problem{1} A continuación se presenta la interpretación geométrica de la solución de la inecuación
\[
2x^3 + 13x^2 - 8x - 46 \geq 6
\]
\begin{figure}[ht]
\centering
\begin{tikzpicture}[scale = .6]
\tkzInit[xmin = -8, xmax = 4, ymin = -100, ymax = 100, ystep = 25]
\tkzAxeXY[label options = {font = {\tiny}}]
\tkzFct[color = myBlue, line width = 1.5pt]{2 * x ** 3 + 13 * x ** 2 - 8 * x - 52}
\draw[line width = 7pt, negative, opacity = .5] (-8, 0) -- (-6.5, 0);
\draw[line width = 7pt, positive, opacity = .5] (-6.5, 0) -- (-2, 0);
\draw[line width = 7pt, negative, opacity = .5] (-2, 0) -- (2, 0);
\draw[line width = 7pt, positive, opacity = .5] (2, 0) -- (4, 0);
\node (i1) at (-7.3, .5) {\textcolor{negative}{\Huge -}};
\node (i1) at (-4.25, .5) {\textcolor{positive}{\large +}};
\node (i1) at (.3, .5) {\textcolor{negative}{\Huge -}};
\node (i1) at (3, .5) {\textcolor{positive}{\large +}};
\end{tikzpicture}
\end{figure}
\switchcolumn
Compruebe los intervalos de solución expresados sobre la gráfica mediante el desarrollo algebraico de la inecuación. Recuerde expresar el intervalo solución en escritura de intervalo, en conjunto y sobre la recta real.
\vskip 3mm
\solution{} \todo[color = orange!75!gray]{\small Si tiene inconvenientes al factorizar el polinomio utilice la regla de Ruffini.}
\end{paracol}
\vskip 3mm
\problem{2} Suponga que $a, b, c$ y $d$ son número positivos tales que
\[
\frac{a}{b} < \frac{c}{d}.
\]
Demuestre que
\[
\frac{a}{b} < \frac{a + c}{b + d} < \frac{c}{d}.
\]
\vskip 3mm
\solution{}
\vspace{30mm}
\problem{3} Responda Verdadero (\textbf{V}) o Falso (\textbf{F}).
\begin{center}
Si $a < b$ y $c < d$, entonces $c - b < d - a$.
\end{center}
Justifique su respuesta, i.e. si su respuesta es Verdadero, explique por qué $c - b < d - a$ cuando $a < b$ y $c < d$; si su respuesta es Falso utilice un contraejemplo i.e. encuentre número $a, b, c$ y $d$ tales que $a < b$ y $c < d$ pero $c - b \geq d - a$.
\vskip 3mm
\solution{}
\vspace{30mm}
\problem{4} La báscula de una tienda está diseñada para que su error máximo sea de 0.25 onza. Si en la báscula se ponen dos latas idénticas de sopa, y su peso combinado es de 33.15 oz. ¿cuáles son los pesos máximo y mínimo que puede tener una de las latas?. De su respuesta en el contexto del problema.
\vskip 3mm
\solution{}
\vspace{30mm}
\problem{5} \marginnote{\includegraphics[scale = 1]{overleaf}} Dada la inecuación $9x - 2x^2 + 9 \geq 0$, construya la gráfica de la parábola y determine los intervalos de solución. Resuelva la inecuación analíticamente y verifique que su interpretación geométrica es correcta.
\vskip 3mm
\solution{}
\vspace{30mm}
\problem{6} \marginnote{\includegraphics[scale = 1]{overleaf}} Construya la gráfica de $|1 - 2x|$ y $\frac{1}{|x|}$ en el mismo plano coordenado. Muestre los intervalos de $x$ en los que tiene solución la inecuación
\[
|1 - 2x| < \frac{1}{|x|}
\]
Compruebe analíticamente expresando su solución en intervalo, conjunto y gráfica de signos.
\vskip 3mm
\solution{}
\vspace{30mm}
\problem{7} \todo[color = cyan!65!gray]{\small Si resuelve este problema su solución será publicada en la cartelera de matemáticas} In any $\triangle ABC$, $E$ and $D$ are interior points of $\overline{AC}$ and $\overline{BC}$, respectively. $\overline{AF}$ bisects $\angle CAD$, and $\overline{BF}$ bisects $\angle CBE$. Prove $m\angle AEB + m\angle ADB = 2m\angle AFB$.
\begin{itemize}
\item[(C1)] Prove that this result holds if $E$ coincides with $C$.
\item[(C2)] Prove that the result holds if $E$ and $D$ are exterior points on extensions of $\overline{AC}$ and $\overline{BC}$ throught $C$.
\end{itemize}
\begin{figure}[ht]
\centering
\begin{tikzpicture}
\coordinate[label = left:{$A$}] (a) at (0, 0);
\coordinate[label = right:{$B$}] (b) at ($(a) + (5, 0)$);
\coordinate[label = above:{$C$}] (c) at ($(b) + (120:4)$);
\coordinate[label = right:{$D$}] (d) at (30:4.3);
\coordinate[label = left:{$E$}] (e) at ($(b) + (150:3.85)$);
\coordinate[label = above:{$F$}] (f) at (40:3.5);
\draw (a) -- (b) -- (c) -- cycle;
\draw (a) -- (d);
\draw (b) -- (e);
\draw (a) -- (f);
\draw (b) -- (f);
\end{tikzpicture}
\end{figure}
\end{document}