overleaf template galleryCommunity articles — Recent
Papers, presentations, reports and more, written in LaTeX and published by our community.

Estudo bíblico baseado no livro: Contracultura Cristã de Jhon Stott.

This is the trials of creating a simple Pong game in six days time. there were severak errors along the way, and the game itself was never actually completed, but it was a fantastic learning experience that will prepare me for future programming courses.
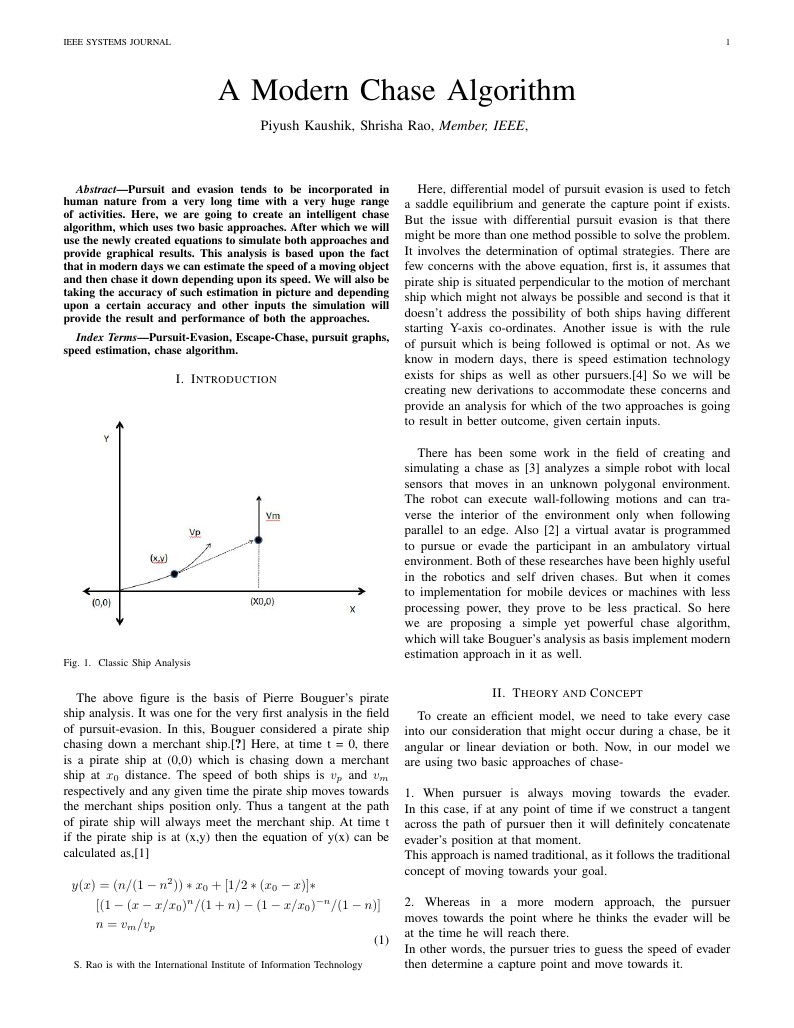
Pursuit and evasion tends to be incorporated in human nature from a very long time with a very huge range of activities. Here, we are going to create an intelligent chase algorithm, which uses two basic approaches. After which we will use the newly created equations to simulate both approaches and provide graphical results. This analysis is based upon the fact that in modern days we can estimate the speed of a moving object and then chase it down depending upon its speed. We will also be taking the accuracy of such estimation in picture and depending upon a certain accuracy and other inputs the simulation will provide the result and performance of both the approaches.

Data warehouse and online analytical processing (OLAP) both are core component for decision making and support which had become focus of attraction in the data base management industry. By increasing demand of these two thing in data base there are now there is much these type of products in commercial and user base and as well as this type of services are available in market as well as to the vendors of data base management systems has offered in these area. Whereas the decision making support have some different requirement in database technology as we can compare with traditional online transaction processing application. In this literature survey data warehousing and OLAP technologies have been gathered with new requirement. The literature survey I have also described about the back end tools which are used for extraction, cleaning and loading into data warehouse and making multidimensional data models typically of the OLAP. Where as in the front end client tools are of the query execution and it also include data analysis where as the server extension are efficient in query processing also in other type of tools for metadata management as well but also for the managing that data ware house.

Sarvesh Parab's Résumé. Created with the Medium Length CV template.

This document aims to recognize the existence of some national health information systems, particularly in the emergency department. Also aims to understand all the functions as well all their interactions with other systems. We enumerate some of these information systems at national level, based our information in instruction manuals, scientific articles and websites of the respective entities. Analysing the whole national reality, we conclude that there are several information systems in the emergency department having as objetive the provision and improvement of health of the patient. This diversity of systems reflects in several problems, like the interoperability, that influences the delivery of care.

Exemple de MCOT pour les TIPE (Travaux d'Initiative Personnelle Encadrés) pour les concours d'entrée aux écoles d'ingénieurs à partir de la session 2017. L'idée est de laisser LaTeX gérer la bibliographie en la complétant au passage via l'utilisation de scholar.google.fr pour les recherches et la récupération des entrée BibTeX comme décrit dans cette vidéo.

My documentation report Objective: Explain what I did and how, so someone can continue with the investigation Important note: Chapter heading images should have a 2:1 width:height ratio, e.g. 920px width and 460px height. Note: This was produced using the Legrand Orange Book template, available here. Original author of the Legrand Orange Book template: Mathias Legrand (legrand.mathias@gmail.com) with modifications by: Vel (vel@latextemplates.com) Original License: CC BY-NC-SA 3.0

This article presents the activities carried out in the compulsory stage for the completion of the Technical Course in Integrated Computing IFRS - Campus Ibirubá . These are focused on software development area, with a brief involvement in the hardware area.
\begin
Discover why over 25 million people worldwide trust Overleaf with their work.