Recent

(A Talk) A brief overview of techniques to understand and remember the unit circle

Cálculo de momento de inercia de un cilindro solido y una esfera hueca

TABLA EQUIVALENCIAS CUANTIFICADORES

Dieses Dokument enthält Notizen aus dem Kurs Mathematik 1 des Studienbefähigungslehrgangs 2014/15 der FH Joanneum Kapfenberg.

The fundamental necessity for water is a widespread issue affecting many communities across the globe. In this project, our team sought to provide an innovative solution to this problem for a small community with access to a relatively close source of flowing water. Resultant flow rate of water was calculated to be 0.498 L/min. Stress and strain analysis on individual subsections of the system were as follows: -44.2 MPa for bending moment in the rod; -7.04 MPa for shear stresses in the rod of the axis; -8.88E-5 for shear strain in the rod ; -1.11 MPa and .429 MPa of shear stresses in the L brackets; -0.123 MPa for radial stress of spiral, -0.422 MPa for hoop stress of spiral, -2.10 MPa for bending moment of spiral, and -0.176 MPa for the maximum shear stress of the spiral pump on the rotating wheel. The focus of the design remained fixated on water acquisition; however, further additions can be made for water purification.

Cour 1 ere AS
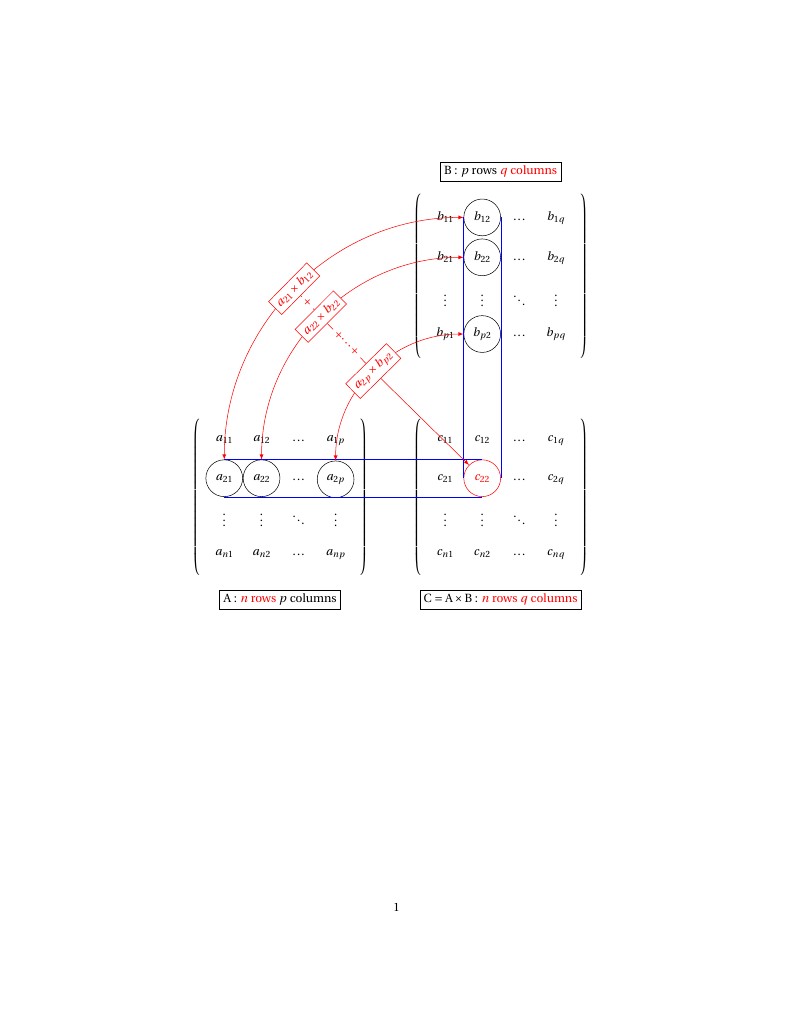
Graphical illustration explaining matrix multiplication

Math 453 HW 1 (with solutions)

Sejarah matematika tidak bisa dilepaskan dari penemuan dan pengembangan bilangan imajiner. Saat ini bilangan imajiner masih digunakan secara luas dalam berbagai bidang, baik untuk keperluan teoritis maupun praktis. Tetapi sedikit orang yang mengetahui kisah dibalik pengembangan bilangan ini yang telah dipenuhi dengan petualangan dan teka-teki. Juga tidak banyak orang yang mengetahui persentuhan penting bilangan imajiner (atau bilangan kompleks) dengan Landasan Matematika, yang memiliki kaitan penting dengan teori filsafat, ilmu logika dan uraian latar belakang sejarahnya.
\begin
Discover why over 20 million people worldwide trust Overleaf with their work.